Most people interested in digital audio know that music is recorded and played back at more than one sample rate. (For an explanation of sample rates, read "Understanding Digital Music -- What Bit Depth and Sample Rate Really Mean: Part Two.) The principal sample rates used today are 44.1, 48kHz and their multiples (i.e., 88.2, 96, 176.4, 192, and so on). CD’s sample rate is 44.1kHz. Sample rates of 88.2kHz and above are considered high-resolution. In both the recording and playback of music, it is often necessary or convenient to switch between sample rates. There are different types of sample-rate conversion, and different ways of going about the process. This article focuses on conversions that take place at the distribution and playback end of the chain -- explaining what the terms mean, what some of the consequences of conversion are, and the implications for a computer-based audio system.
However a piece of music was recorded, or the various twists and turns it may have taken along its path, there is ultimately a studio master at some particular sample rate. The best state of affairs is for you to obtain an exact copy of that master. Often, however, the distribution medium is incapable of carrying that format -- e.g., the CD’s limit of 44.1kHz precludes higher sampling rates -- or someone makes a business decision to release the recording in a sample rate other than the native one. On the playback side, not all equipment or transfer protocols support all sample rates. Some manufacturers and consumers also believe that there are benefits to changing the sample rate of a recording on playback -- a matter I address below.
At the highest level, there are only two types of sample-rate conversion. In upsampling, the output sample rate is higher than the input sample rate. In downsampling, the output sample rate is lower than the input sample rate. Before a signal can be downsampled, it must be low-pass filtered in order to avoid aliasing. The two-step process of filtering and downsampling is called decimation. Special instances of these conversions are oversampling and undersampling, wherein the input and output sample rates are related by an integer factor -- e.g., 44.1 and 88.2kHz. In all other cases -- e.g., between 44.1 and 96kHz -- it is called arbitrary sample-rate conversion (ASRC). You may find other usages of these terms, but these are the definitions to which I adhere in this article. They are also consistent with the usage in a more technical explanation of the subject that can be found here.
Imagine that we have an 88.2kHz digital master that we would like to put on a CD with a 44.1kHz sampling frequency. The situation is the same if we have an 88.2kHz file that we’d like to play through a DAC that supports sample rates up to only 44.1kHz. After employing a digital low-pass filter to suppress frequencies above half the 44.1kHz sample rate -- i.e., frequencies above 22,050Hz -- we can simply drop every other sample to arrive at the new sample rate. Information above 22,050Hz is thrown away and can never be recovered.
In the other direction, imagine a 44.1kHz source we would like to convert into an 88.2kHz output. The simplest way is to use a linear interpolation algorithm, which inserts, between each pair of consecutive samples, an additional data point with a value halfway between the two original samples. A higher-order interpolation algorithm could be used to better predict the value of the original signal. Oversampling to higher multiples of the input sample rate just requires more interpolations. Although, at the end of the process, we have more data points, the signal contains no additional or "restored" information. No matter how many times we oversample a 44.1kHz source signal, there will still be no frequencies above 22,050Hz (though a poorly implemented algorithm could add high-frequency noise). The reason most DACs oversample the signal is to spread out quantization noise, increase the effective resolution, and allow for the use of a gentler analog low-pass filter at the output.
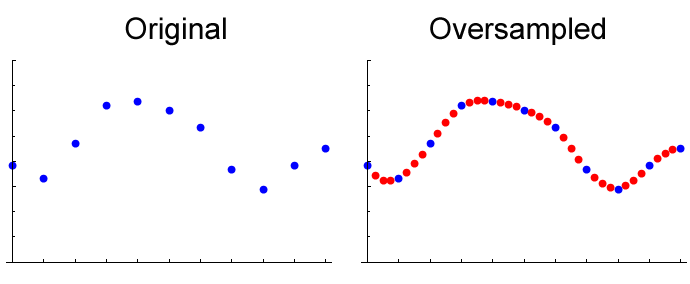
Left: Original samples of a signal. Right: Same samples along with the additional samples generated by 4X oversampling using third-order interpolation. The oversampled curve looks smoother, but no additional information has been added.
When we want to do a non-integer sample-rate conversion, things get much more complicated. For real-time systems, the solution is to use clocks running at the two different sample frequencies. If the relationship between the two sampling frequencies is fixed, then we simply oversample the input signal to the least common multiple of the two sample rates -- for 44.1 and 96kHz, that is 14.112MHz, or 320-times oversampling -- then decimate to the output frequency. This process requires that the two sample clocks be perfectly synchronized; for example, using a phase-locked loop (PLL).
The trouble is that in most implementations, especially the ones that can be bought on a single chip, the clocks are not synchronized but independent. This is called asynchronous sample-rate conversion (ASRC), or, better, arbitrary asynchronous sample-rate conversion (AASRC). Both clocks wander with respect to real time and to each other. The result is that we probably need the value for the signal either just before or just after the data point we’ve created by oversampling the input to the least common multiple. If we just take the nearest sample, we’ve added distortion. The solution is to oversample much faster in order to create something approaching a continuous time signal. This approach is analogous to doing a digital-to-analog conversion followed by an analog-to-digital conversion, except that the entire process takes place in the digital domain. The oversampling ratio required to reduce the timing distortion to acceptable levels is huge. Instead, a lower oversampling ratio is used, and a second interpolation filter between the samples where we need it. A circuit tracks the relationship between the two clocks, and picks the right value from the interpolated data. The actual designs of the oversampling/interpolation stage and the frequency tracker become very complex and are beyond the scope of this article. It is sufficient to know that careful design of these elements can reduce the distortion inherent to AASRC, but not entirely eliminate it.
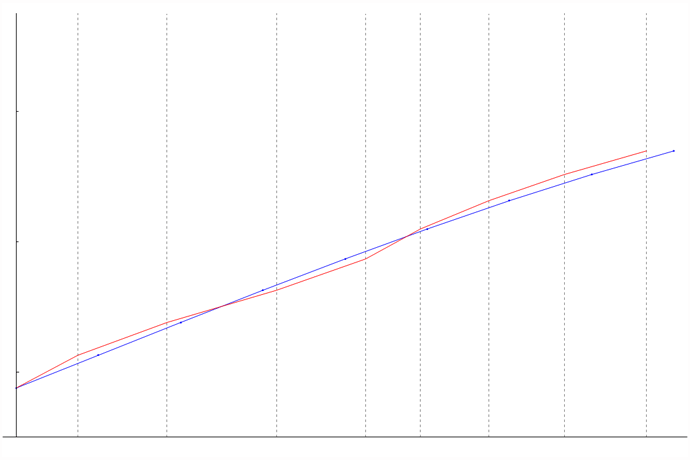
The graph shows an upsampled signal in blue. The vertical dashed lines show where an unsynchronized clock tries to take the data. The difference in value, on the vertical axis, between where the dashed line crosses the signal's line and the closest available sample -- represented by a dot -- is error that distorts the resampled signal. The resulting distorted signal is shown in red.
If AASRC introduces distortion, why would we ever want to do it? Some manufacturers make the claim that upsampling a 44.1kHz source to 96kHz or higher restores information that was lost when the digital master was downsampled for release on CD, but that is nonsense: Once the information is lost, you can never get it back. Other manufacturers claim that upsampling the signal spreads out quantization noise and allows for gentler analog filtering of the DAC’s output. You might recognize those benefits as the same reasons given for oversampling. That is because oversampling provides those same benefits, but without the distortion and timing errors inherent in asynchronous upsampling.
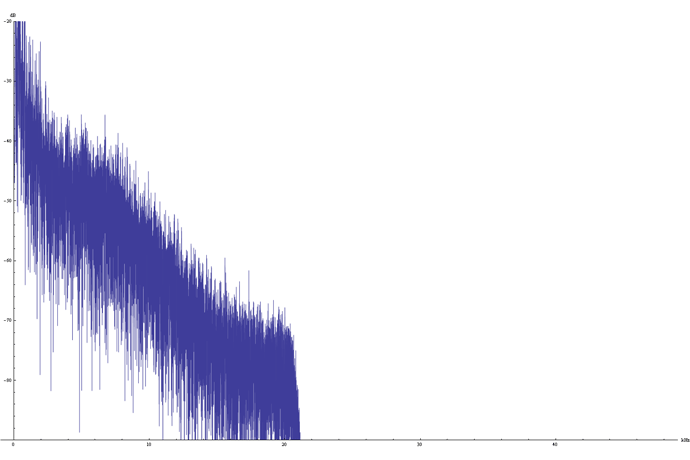
The graph shows the frequency spectrum of a 44.1kHz source that has been upsampled to 96kHz. Note that there is no frequency information above half the original sample rate (i.e., 22,050Hz).
There are, however, legitimate reasons why one might want or need to asynchronously convert a digital signal. Sometimes the DAC chip is capable of operating only at multiples of 48kHz, or at least it performs better that way due to the characteristics of its clock. An asynchronous sample-rate converter can also filter out jitter in the incoming signal, but not eliminate it entirely. The degree to which an AASRC can suppress jitter depends on its specific design. These potential benefits must be considered against the timing inaccuracies introduced by the asynchronous clocks.
My experience -- and that of SoundStage! Network publisher Doug Schneider and editor Jeff Fritz -- is that AASRC generally sounds worse than playing audio at its native sample rate. However, there are many different implementations of AASRC, so results do vary. In some cases the difference in sound quality is very small, and we do not rule out the possibility that a DAC employing AASRC could sound better than one that does not. As a matter of philosophy, we’d like to see as little math performed on the signal as possible. Therefore, we advocate using native sample rates or integer conversions for playback.
It is important to remember that not all arbitrary sample-rate conversions are asynchronous. When the conversion is done offline -- e.g., by a computer during the mastering process -- there is no sample clock at all, and the data can be interpolated to provide the value of the signal at exactly the desired sample time. In such a scenario, non-integer sample-rate conversion is really no different from integer sample-rate conversion, provided a good algorithm is used. There are some examples in which this approach has been taken. Many reviewers and audiophiles, including me, have praised the recordings from Norwegian record label 2L. Most of these recordings were made at 352.8kHz, but are distributed as 96 and 192kHz files for two reasons. One is that there are a number of computer-connected DACs that would not support the integer-converted sample rates of 88.2 and 176.4kHz. The other is that many of these recordings are also distributed on Blu-ray Discs, a format that does not support 88.2 or 176.4kHz. We know that 2L uses Weiss Saracon software, which does an exact conversion using least common multiples. Therefore, there should be no penalty in converting to 192 rather than 176.4kHz, and the results speak for themselves.
These findings suggest that if you have 88.2kHz files and a DAC that supports only the 96kHz sample rate, better performance may be obtained by converting those files to 96kHz offline rather than relying on whatever algorithm the playback software is using to do the conversions for you. A computer has sufficient horsepower to do asynchronous sample-rate conversion in real time, but I’m not aware of any playback software that implements an exact, transparent conversion. It is also interesting to consider that a DAC with sufficiently high processing power, a buffer system, and reclocking could do similar arbitrary sample-rate conversions without them being asynchronous.
Sample-rate conversions aren’t necessarily bad. In some cases they are necessary, and in many they do improve the quality of the output signal. It's important to recognize the difference between the various forms of sample-rate conversion in order to select intelligent trade-offs.
. . . S. Andrea Sundaram
andreas@soundstagenetwork.com
