Not long ago I was having a conversation with some fellow audiophiles about a recording with a five-string bass guitar that went down to 30Hz -- actually 30.87Hz, which is the lowest B on the standard piano keyboard. Most of them thought that made it an excellent track for assessing the bass performance of a system, but I disagreed. While there’s no question that this track and others like it sound more impressive the deeper the playback system can go, the fact that you can hear those low notes doesn’t mean the system has a flat frequency response down to 30Hz. Let’s take a look at why.

When any real instrument produces a note, there’s more frequency content than just the fundamental. A 30Hz tone will also contain energy at 60Hz, 90Hz, 120Hz, and so on. The relative amplitudes of these harmonics are what give the instrument its timbre. When the ear-brain system receives this collection of soundwaves, it’s interpreted as a single note. If there’s variation in the amplitudes of the various components, it merely changes the character of the instrument. Even when the fundamental is almost completely absent, your brain knows to fill it in. That’s why when you’re listening to small speakers that only go down to, for example, 70Hz, you can still follow the bassline of any song.

In the following graph, I’ve constructed a hypothetical bass tone consisting of the fundamental at 55Hz -- the A two octaves below middle C -- and its first five harmonics going up to 330Hz. The relative amplitudes of the harmonics are typical for an acoustic bass. There are lines showing the waveform with zero attenuation of the fundamental, 3dB, and 6dB. You can clearly see that the waveform changes, and by clicking on the appropriate link below the graph you can also hear a two-second clip of each sound.

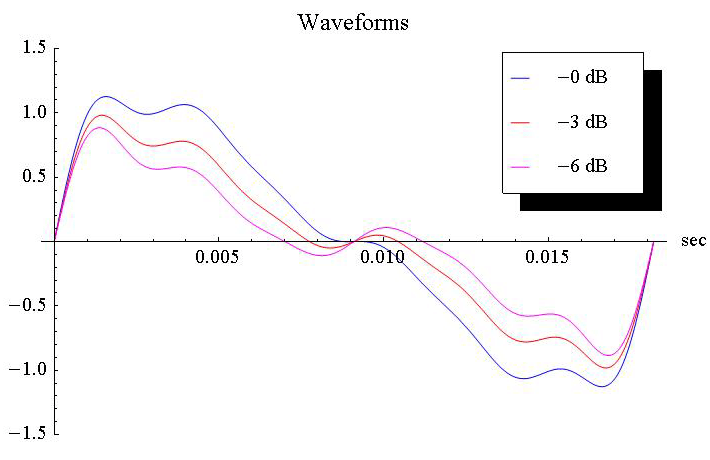
• 55Hz, -0dB -- a 55Hz tone with its first five harmonics with no attenuation of the fundamental (download 175k WAV file) 
• 55Hz, -3dB -- fundamental attenuated by 3dB (download 175k WAV file)
• 55Hz, -6dB -- fundamental attenuated by 6dB (download 175k WAV file)

I also created a small program that lets you do your own experimentation. You can manipulate the fundamental frequency and then attenuate the fundamental to whatever level you like. The program will display the graph and generate a sound that you can hear. Of course, you’ll get the best results if your computer is connected to your hi-fi, but good headphones or very good computer speakers will also yield meaningful results. In order to run the application, you'll need to download the free Mathematica Player software.

• Download Bass Tone Generator application for Mathematica Player (right-click and "Save As")

There are two good ways to use this program, and you’ll gain the best understanding of the subject by trying both. In a system that has flat bass extension down to below the level where you set the fundamental frequency, you’ll be best able to assess what degree of attenuation really makes an audible difference. In a system with smaller speakers, you likely won’t hear much difference unless you severely attenuate the fundamental frequency component. For those who have smaller speakers -- that’s me most of the time -- you can achieve a rough approximation of the differences you would hear on a bigger system by setting the fundamental frequency in a range where your speakers are still flat. Even though mathematically that situation is identical, it doesn’t quite sound the same -- probably because of the physical nature of very low frequencies.

The right way

The best way to examine the bass performance of your system is to measure it. The software and hardware for taking these measurements has become fairly inexpensive, but they’re still probably not justified unless you’re an audio reviewer who’s constantly assessing new products. The next best way is to use test tones that are based on pure sinewaves. A pure 30Hz tone, by definition, includes no other frequencies to confuse the issue -- actually, there will be some extremely minor contributions from various types of distortion in the system. You could use a sound-pressure-level meter to measure these test tones, as long as you’re sure that it has a flat frequency response. I find it nearly as useful to just listen. In fact, some might argue that listening is the more valid approach, because it includes the all-important aspect of perception. It depends on whether you think a system should measure flat or sound flat, and whether or not there’s a difference between the two.

CDs of test tones are available from a variety of sources, but we at the SoundStage! Network don’t like to waste our money on buying test tones when we could be buying music, and we don't think you should have to either. That’s why we’ve created a few files that you can download and use to test your own system. If your computer is connected to your hi-fi, you can run them directly. Otherwise, just burn them to a CD. They’re all monaural WAV files, which are rendered at 44.1kHz -- since we’re talking about continuous bass frequencies, there’s no need for a higher sample rate.

• 200 -- frequency steps down in 10Hz increments from 200Hz to 110Hz (download 1.75MB WAV file)
• 100 -- frequency steps down in 10Hz increments from 100Hz to 10Hz (download 1.75MB WAV file)
• 50 -- frequency steps down in 5Hz increments from 50Hz to 5Hz (download 1MB WAV file)
• 200s -- frequency sweeps down from 200Hz (download 1.75MB WAV file)
• 400s -- frequency sweeps down from 400Hz (download 0.7MB WAV file)

Three of the files step down in frequencies so that you can assign a relatively precise numerical value to where your system drops off in bass response. The other two are downward frequency sweeps, which serve to identify where your bass response might have peaks or troughs. These test tones are useful not only for assessing the inherent qualities of a component or system but also for positioning speakers in a room or even integrating a subwoofer -- just listen for where everything sounds even.

Of course, there’s more to bass performance than simple frequency response, and for that you need to listen to a variety of music -- which is hardly a hardship.

. . . S. Andrea Sundaram
andreas@soundstagenetwork.com